理解贝塞尔曲线原理

发表于 | 更新于: | 分类于 | |

贝塞尔曲线为绘制平滑曲线提供了数学理论，也是很多动画绘制的基础，在我们前端开发的过程中也常常使用它控制动画的执行速度（animation-timing-function）。那么这个曲线实现的原理是什么呢，让我们一探究竟吧。

原理

贝塞尔曲线的轨迹由多个控制点决定，根据控制点的多少可以分为一阶、二阶、三阶以至于 n 阶的贝塞尔曲线。

一阶

一阶贝塞尔由 2 个控制点 P0 和 P1 构成，公式如下

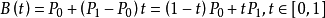
由公式可以看出，B(t)绘制出来的应该是一条直线，所以一阶公式也称为线性公式。

我们也可以简单看出绘制的原理，在 P0 和 P1 直接有个移动的点，从 P0 作为起点，随着时间的推移，慢慢向 P2 移动，移动的轨迹就是得到的曲线。

二阶

二阶贝塞尔有 3 个控制点 P0，P1 和 P2 构成。多介的贝塞尔的是由一阶的“无限套娃”所计算出来的。比如二阶有 3 个控制点，相邻的控制点可以组成一条线段：P0-P1 和 P1-P2。那么 P0-P1 和 P1-P2 又可以视作一阶的贝塞尔，从而获取到曲线的移动点。

让我们简单用数学计算一下

1
2
3
4
5
6
B(t01) = (1-t)P0 + tP1
B(t12) = (1-t)P1 + tP2
B(t) = (1-t)B(t01) + t(B(t12))
= (1-t)((1-t)P0 + tP1) + t((1-t)P1 + tP2)
= (1-t)^2P0 + tP1 -t^2P1 + tP1 - t^P1 + t^2P2
= (1-t)^2P0 + 2t(1 - t)P1 + t^2P2

套用公式，我们可以得到轨迹图如下

多阶

有了二阶的经验，三阶四阶乃至多阶贝塞尔计算思路都很清晰了。多阶可以通过降解成一阶贝塞尔，所以我们可以使用递归来计算多阶贝塞尔曲线的轨迹值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class ControlPoint {
  constructor(public x: number, public y: number) {}
}

function getBezierPoint(points: ControlPoint[], t: number) {
  const l = points.length;
  if (l > 1) {
    const nextPoints = [];
    for (let i = 0; i < l - 1; i++) {
      const p1 = points[i];
      const p2 = points[i + 1];
      nextPoints.push(getNewPoint(p1, p2, t));
    }
    return getBezierPoint(nextPoints, t);
  }

  return points[0];
}

function getNewPoint(p1: ControlPoint, p2: ControlPoint, t: number) {
  const x = p1.x + (p2.x - p1.x) * t;
  const y = p1.y + (p2.y - p1.y) * t;
  return new ControlPoint(x, y);
}

于是我们可以到下面这些绝妙的曲线

三阶贝塞尔

四阶贝塞尔

css3 中的 bezier

css3 中我们使用的是三阶贝塞尔，即有 4 个控制点。css 已经帮我预设了 (0, 0) 和 (1, 1) 两个控制点，一个是 P0 开始节点，一个 P3 结束的节点，所以我们只需传入 2 个节点即可。

源码和在线 demo

如果无法打开，请翻墙。